Vorhersagen in der Energiewirtschaft – Welche Methoden eignen sich?

In diesem Beitrag geht es um Vorhersagen bzw. Prognosen in der Energiewirtschaft. Im vorherigen Beitrag haben wir uns allgemein mit Metriken befasst, die sowohl für Regressions- als auch für Klassifikationsaufgaben verwendet werden können. Im Folgenden liegt der Fokus speziell auf der Vorhersage von Zeitreihen, die in der Energiewirtschaft häufig anzutreffen sind. Allgemein versteht man unter einer Zeitreihe eine Folge an reellen Zahlen x_t₁, …, x_tₙ welche zu den Zeiten (t₁,…,tₙ) aufgenommen wurden. Beispiele in der Energiewirtschaft sind der Energiepreis, die Produktion oder der Verbrauch von Energie, ob ein Elektrofahrzeug zu einem Zeitpunkt eingesteckt ist oder wie der Füllstand eines Pumpspeicherkraftwerks ist. Um eine Orientierungshilfe bei der Auswahl geeigneter Methoden für die Vorhersage einer spezifischen Zeitreihe zu bieten, haben wir am Ende des Artikels einen Entscheidungsbaum erstellt. Dafür sollte man zunächst die Zeitreihe näher betrachten und ihre Eigenschaften kennenlernen.

Parametrisch/ Nicht-Parametrisch

Bevor man Annahmen über Zeitreihen trifft, ist es wichtig sich zu überlegen, ob man überhaupt Annahmen über die Zeitreihe treffen will. Parametrische Modelle treffen Annahmen über die Zeitreihe, wie zum Beispiel ihre zugrunde liegende Verteilung oder ihre funktionale Form, welche diese durch eine Anzahl an Parametern beschreibbar machen. Dadurch lassen sich die parametrischen Modelle leicht interpretieren, außerdem benötigen sie in der Regel auch einen geringeren rechnerischen Aufwand. Allerdings müssen die Annahmen auch zutreffen, damit das Model eine gute Vorhersage treffen kann. Daher kann es einfacher oder von Vorteil sein, keine Annahmen über die Zeitreihe zu treffen. Hierfür können nicht-parametrische Modelle genutzt werden. Zwar müssen bei nicht-parametrischen Modellen keine Annahmen über die Zeitreihe getroffen werden, dafür sind sie in der Regel aber rechnerische aufwändiger und weniger leicht zu interpretieren. Für die Wahl des richtigen nicht-parametrischen Modells ist primär die Eigenschaften des Modells entscheidend, während bei den parametrischen Modellen die Eigenschaften der Zeitreihen ausschlaggebend ist. Auf die Eigenschaften der Zeitreihe gehen wir im Folgenden ein.

Linear/Nicht-Linear

Die Abhängigkeiten innerhalb einer Zeitreihe sind eine wichtige Eigenschaft, um den weiteren Verlauf einer Zeitreihe zu beschreiben. Eine Zeitreihe wird linear genannt, wenn eine lineare Abhängigkeit zwischen  und den vorherigen Punkten besteht. Eine Zeitreihe ist nicht-linear falls eine andere Abhängigkeit besteht. Bei Zeitreihen ist es unter Umständen sehr schwierig eine klare Aussage zu treffen, ob sie linear oder nicht-linear sind. Möglichkeiten dies zu testen, sind die Autokorrelationsfunktion (ACF) und die Partieelle Autokorrelationsfunktion (PACF), welche bei linearen Zeitreihen typischerweise relativ schnell abfallen (Abbildung 1). Eine weitere Möglichkeit ist der Box-Pierce Test, welcher die Residuen eines linearen Models auf Autokorrelation testet. Falls hier signifikante Autokorrelationen festgestellt werden, ist eine mögliche Erklärung, dass die Zeitreihe nicht-linear ist.

Uni-/ Multivariant

In den meisten Fällen ist es ausreichend eine Zeitreihe mit einer Zielvariablen pro Zeitschritt vorherzusagen.  Eine solche Zeitreihenvorhersage heiß Univariant. Allerdings kann es auch nützlich sein mehrere voneinander abhängige Zielvariablen vorherzusagen. Beispielsweise ist es wichtig nicht nur zu wissen, wann ein Fahrzeug ein und aussteckt, sondern auch, wie seine prognostizierte Lastnachfrage aussieht. Solche Zeitreihenvorhersagen nennt man Multivariant.

Exogene Daten

Häufig sind weitere Informationen zur Vorhersage einer Zeitreihe nützlich und nicht nur die Zeitreihe selbst, da unter Umständen Korrelationen zwischen der Zielvariable und einer unabhängigen (exogenen) Variable bestehen. Deshalb nutzt man häufig exogene Daten, um die Vorhersagen von Zeitreihen zu verbessern. Beispiele hierfür sind bei der Vorhersage des Wärmebedarfs die Miteinbeziehung der Temperatur oder bei der Vorhersage der Energieproduktion durch Windkraft die vorhergesagten Windstärken. (Manchmal sind diese exogenen Daten allerdings nicht vorhanden oder es kann auch hilfreich sein ihren Einfluss bei der Vorhersage nicht zu berücksichtigen.)

Stationär

Die Stationarität einer Zeitreihe beschreibt, wie sie sich ihr zugrundeliegender stochastischer Prozess entwickelt. Genauer ist eine Zeitreihe stationär, falls ihre Wahrscheinlichkeitsverteilung unter Zeittranslation invariant ist. Vereinfacht bedeutet das unter anderem, dass sich der Mittelwert und die Varianz der zugrunde liegenden Verteilung der Zeitreihe sich über die Zeit nicht verändert. Eine Möglichkeit, um zu testen, ob ein Zeitreihe stationär ist, ist der Augmented Dickey-Fuller (ADF)-Test welcher die Zeitreihe, mit der Nullhypothese nicht-stationär zu sein, testet. Typische nicht stationäre Eigenschaften sind Trends oder Saisonalitäten. Diese kann man allerdings häufig durch geschickte Transformationen beseitigen, um auch Methoden zu nutzen die eigentlich nur für stationäre Zeitreihen geeignet sind.

Trends und Saisonalitäten

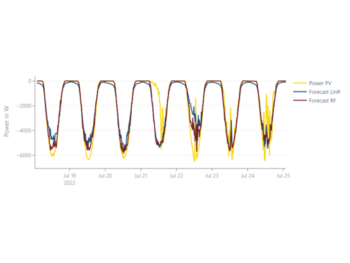
Viele Zeitreihen besitzen sogenannte Trends oder Saisonalitäten, wie beispielsweise in Abbildung 2. Ein Trend beschreibt langfristige Veränderungsmuster im Zeitverlauf. Wenn man sich die in den letzten Jahren durch Photovoltaik erzeugte Energie ansieht, ist zum Beispiel ein deutlich steigender Trend erkennbar. Saisonalität beschreibt Variationen, die in regelmäßigen Abständen auftreten. Dies kann einen täglichen oder wöchentlichen typischen Verlauf bedeuten, aber es können auch über ein Jahr oder Jahre hinweg saisonale Unterschiede erkennbar sein. Beispiele für Zeitreihen mit saisonalen Verläufen in der Energiewirtschaft sind der höhere Wärmebedarf im Winter oder der Strompreis, der durch die PV-Einspeisung in der Mittagszeit deutlich sinkt.

Eigenschaften der nicht-parametrischen Modelle

Für die nicht-parametrischen Modelle sind einerseits die Anforderungen an das Modell wichtig, aber auch die Menge an Daten, die zur Verfügung stehen. Es ergeben sich die folgenden Entscheidungskriterien:

• Die Anzahl der Datenpunkte der Zeitreihe. Ein kleines Datenset umfasst weniger als mehrere tausend Datenpunkte.
• Der rechnerische Aufwand der aufgewendet werden muss.
• Der Implementierungsaufwand, der aufgewendet werden muss, um das Modell zu erstellen. Allerdings sind auch hier teilweise vordefinierte Modellarchitekturen in Form von s.g. Packages (bspw. Sci-kit learn in python)

Darüber hinaus wird angegeben, welche Modelle darauf ausgelegt sind, Sequenzen vorherzusagen und sie als Input zu verwenden. Eine Sequenz bezieht sich in diesem Zusammenhang auf mehrere aufeinanderfolgende Zeitschritte innerhalb einer Zeitreihe. Die Verwendung von Sequenzen kann in der Vorhersage von Zeitreihen vorteilhaft sein, da möglicherweise Wechselbeziehungen oder Muster innerhalb der Serie vorhanden sind.

Entscheidungsbaum – Welche Methoden eignen sich?

Der Entscheidungsbaum soll als Orientierungshilfe dienen, um die passende Methode für die vorliegende Zeitreihe zu finden. Hier kann man überprüfen, welche Eigenschaften die Zeitreihe oder die Methode haben soll, und so zu den Methoden gelangen, die zu den ausgewählten Eigenschaften passen.

Weitere Informationen 

• Vorhersagen in der Energiewirtschaft – Tutorial zur Vorhersage von Haushalts- und PV-Lastgängen
• Vorhersagen in der Energiewirtschaft – Welche Fehlermetriken eignen sich? 
• Vorhersagen in der Energiewirtschaft – Vergleich von konventionellen Machine Learning Methoden und Deep Learning 
• Grundlagen künstlicher Intelligenz und Machine Learning in der Energiewirtschaft 
• Anwendungsfälle von Supervised Machine Learning in der Energiewirtschaft 
• Supervised Machine Learning 
• Bidirektionales Lademanagement (BDL) 

Literatur

[1] Box, G. E. P., Jenkins, G. M., & Reinsel, G. C. (2013). Time Series Analysis: Forecasting and Control (4th ed.). Wiley.

[2] Brockwell, P. J., & Davis, R. A. (2016). Introduction to Time Series and Forecasting. Springer.

[3] Paul, M., Krishnaswamy, S., & Athiyarath, S. (2020). A comparative study and analysis of time series forecasting techniques. SN Computer Science, 175/2020.

[4] Souzaa, V. M. A., Batistaa, E. A. P. A., & Parmezana, A. R. S. (2019). Evaluation of statistical and machine learning models for time series prediction: Identifying the state-of-the-art and the best conditions for the use of each model. Information Sciences, 484.

[5] Das, M., & Gosh, S. K. (2017). Data-driven approaches for meteorological time series prediction: A comparative study of the state-of-the-art computational intelligence techniques. Elsevier.

[6] Tsay, R. S., & Chen, R. (2019). Nonlinear Time Series Analysis. Hoboken, NJ, USA: John Wiley & Sons.